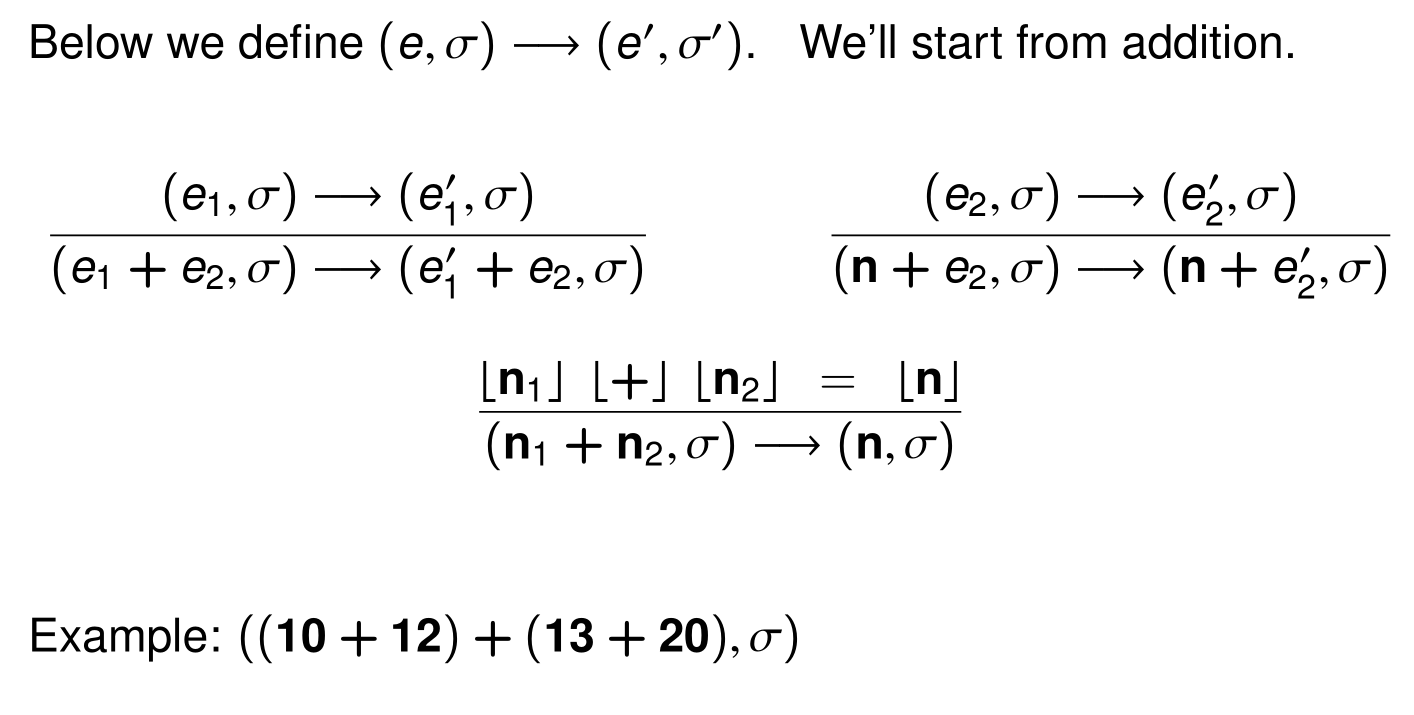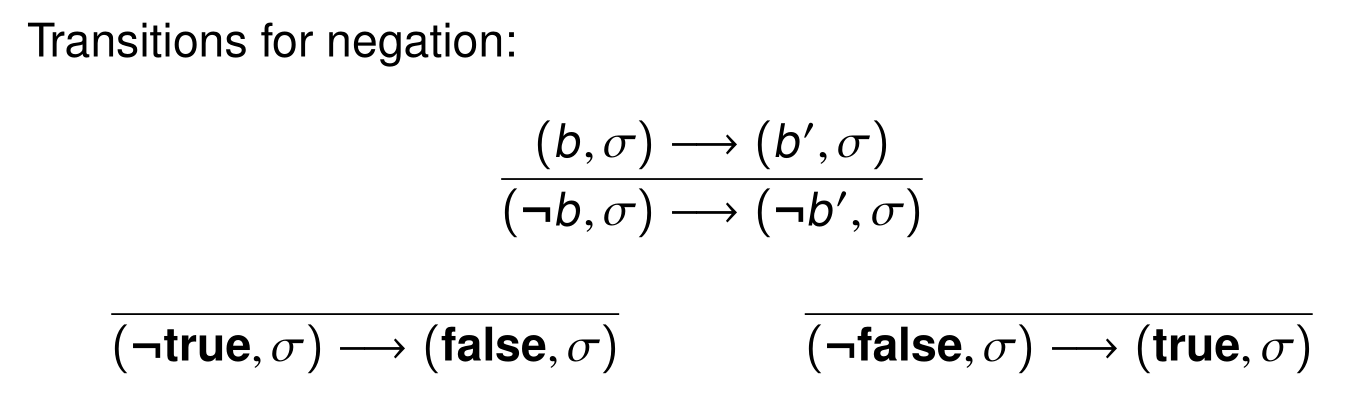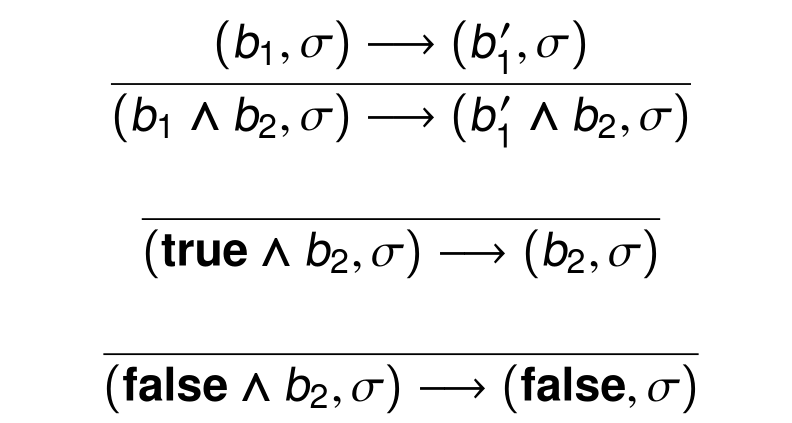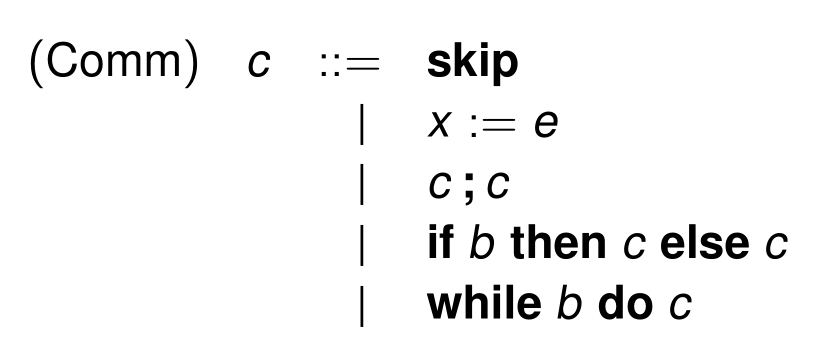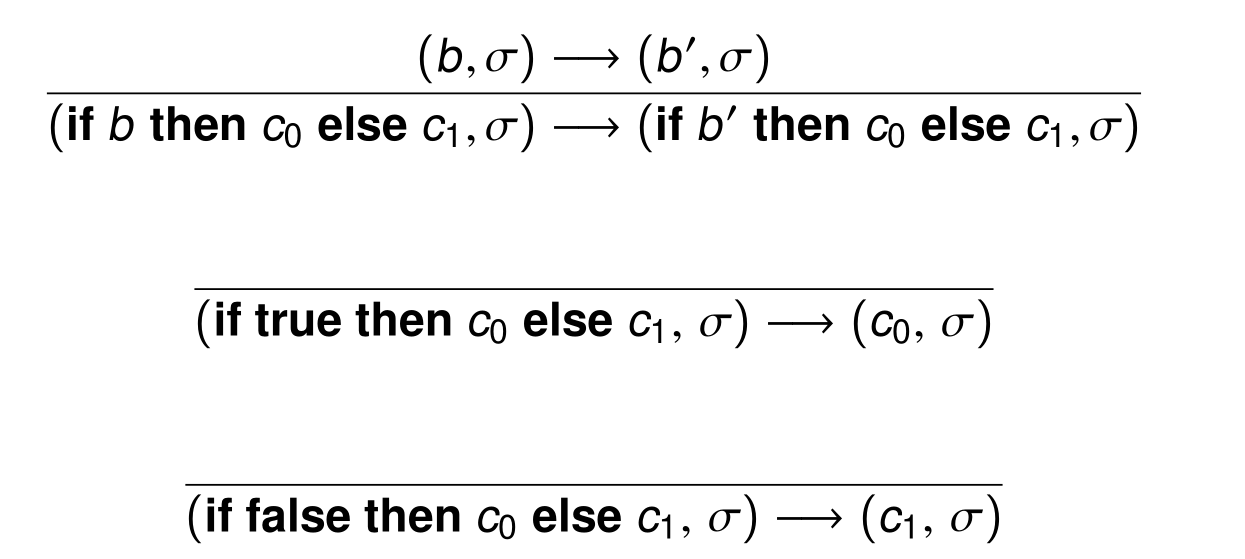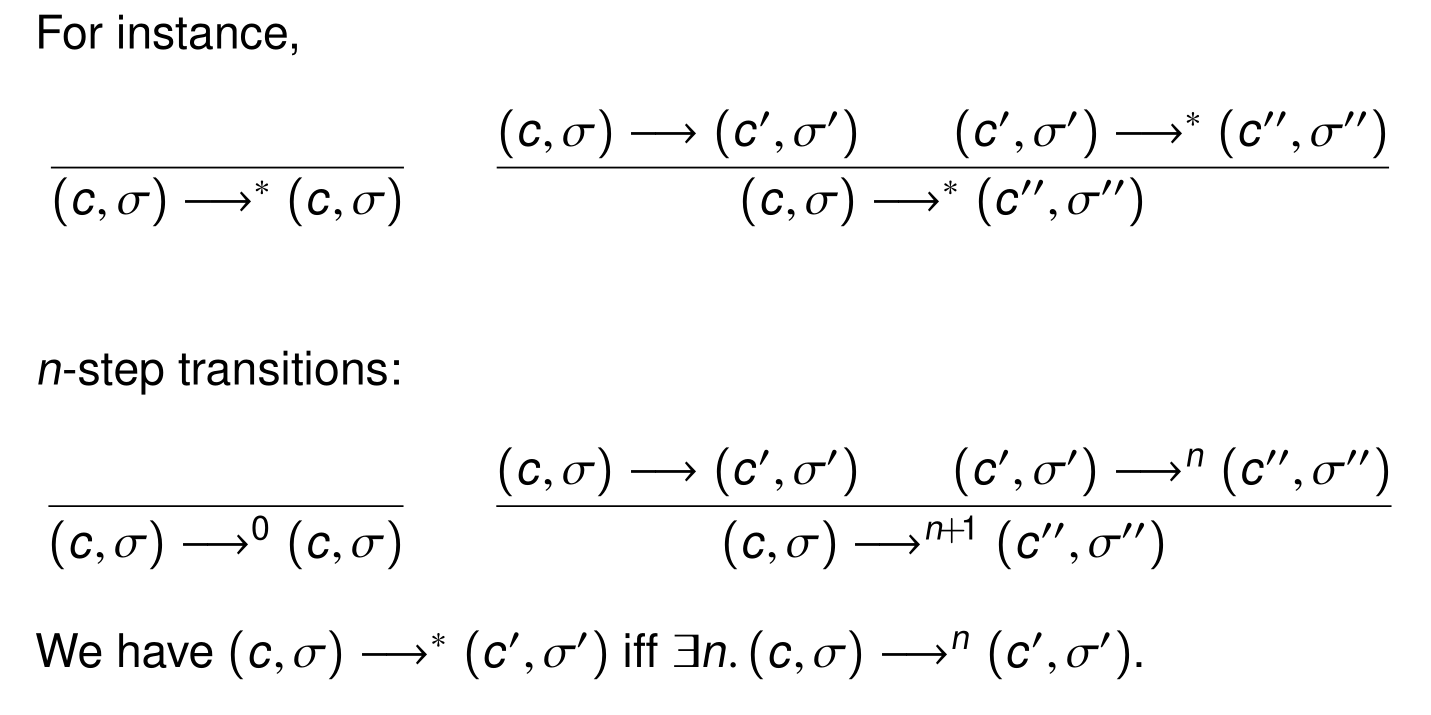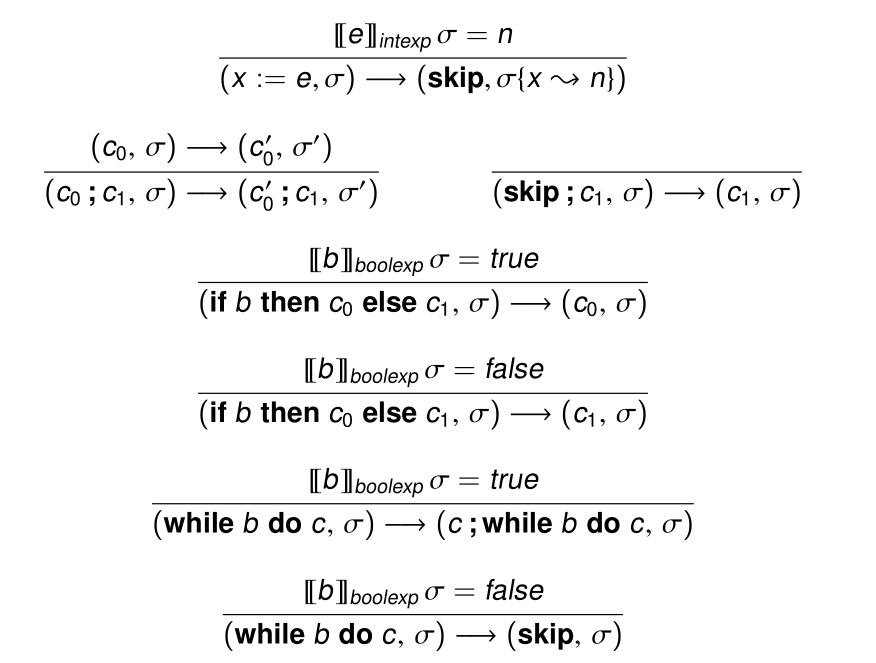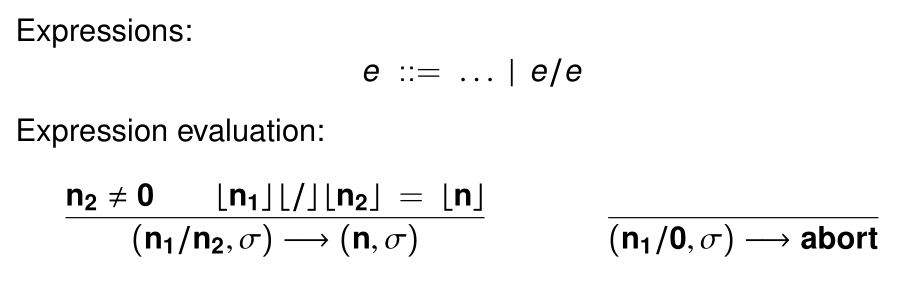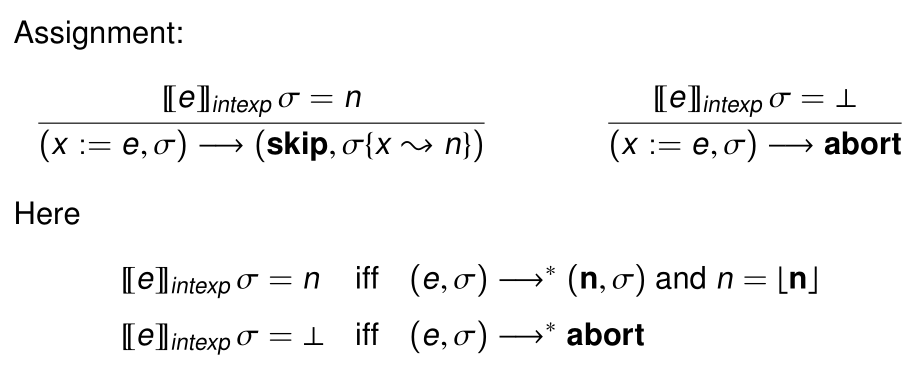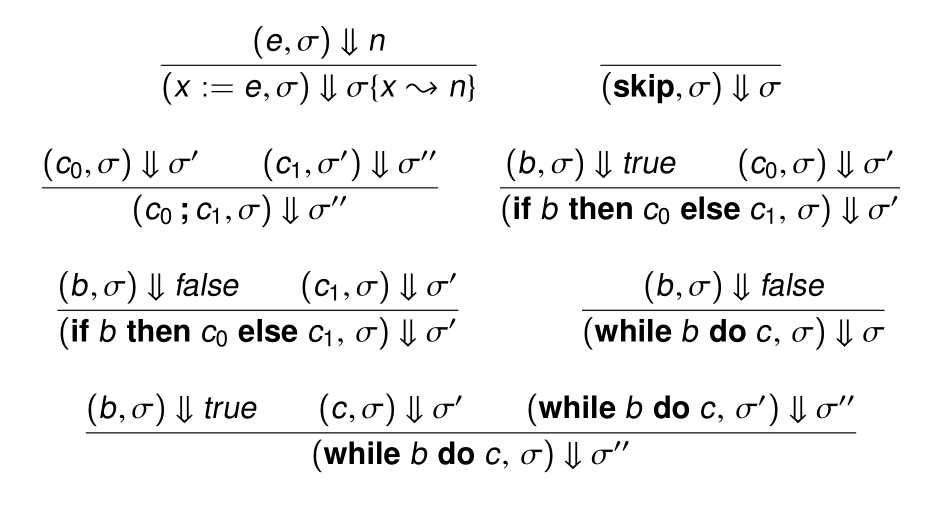之前我们讨论的都是Functional language,现在换个课题,讨论Imperative language(命令式语言)。
在命令式语言中,形式语义共有三种:
- Operational Semantics:操作语义,程序如何一步步的执行。
- Denotational Semantics:指称语义,将程序指称到数学对象上(如tree list)。
- Axiomatic Semantics:公理语义,推导程序性质的证明系统。
我们仅讨论操作语义,其定义了程序的执行过程,形式化就是对一个抽象状态机的转移过程,其中包含:
- Expression/Steatement,即被求值/执行的部分
- States,对Reg/Mem/Data Structure的抽象。
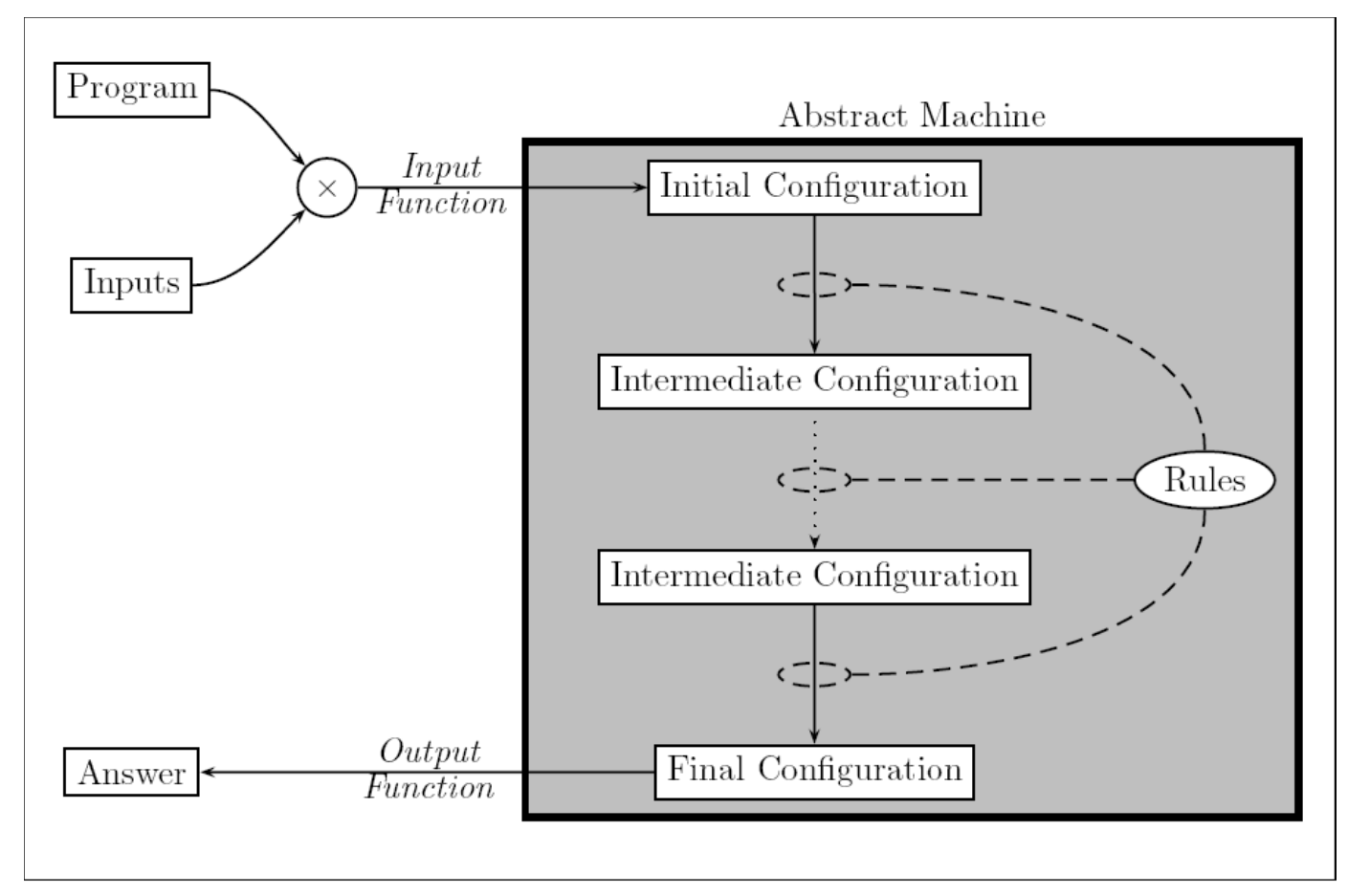
操作语义包含两种方式的定义:
- Small-Step semantics,定义了每一步执行
- Big-Step semantics,定义总体的执行。
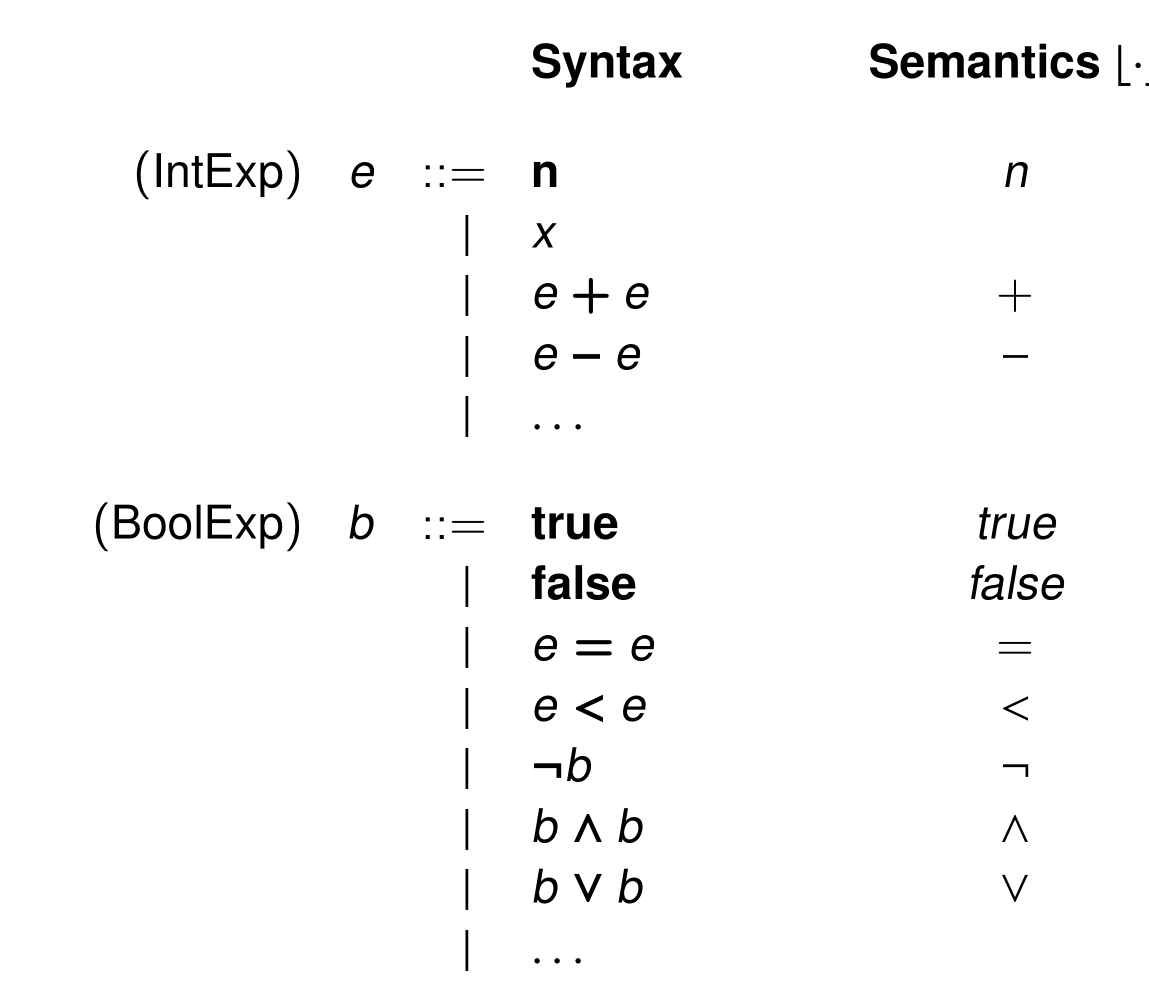
Syntax

上图中,加粗的n表示numerals,只是用于Syntax的描述,注意和自然数进行区分(即需要区分Syntax和Semantics)。
现定义⌊n⌋为b的具体意义,在本章的讨论范围内,⌊n⌋=n,即自然数。
State
既然我们要在命令式语言里进行求值/操作,那么就必须要知道目前的State。
(State)σ∈Var→Values
Value既可以是numeral,也可以是自然数。在本章中,Values表示自然数/Bool值等。
下图为State的操作部分。

在操作语义中,通过不同方式定义的State会和不同的term联合起来作为config。这部分放在下章讨论。
Small-Step Operational Semantics
Structual Operational Semantics(SOS)
程序的语法是通过归纳定义的,从而我们也可以通过定义程序的各部分语义来定义总体的语义。于是就有了SOS。
在这里,Structual代表着“面向语法和归纳”,遵循着严格的顺序和各部分分解执行。
比如,对Syntax中的IntExp,有:
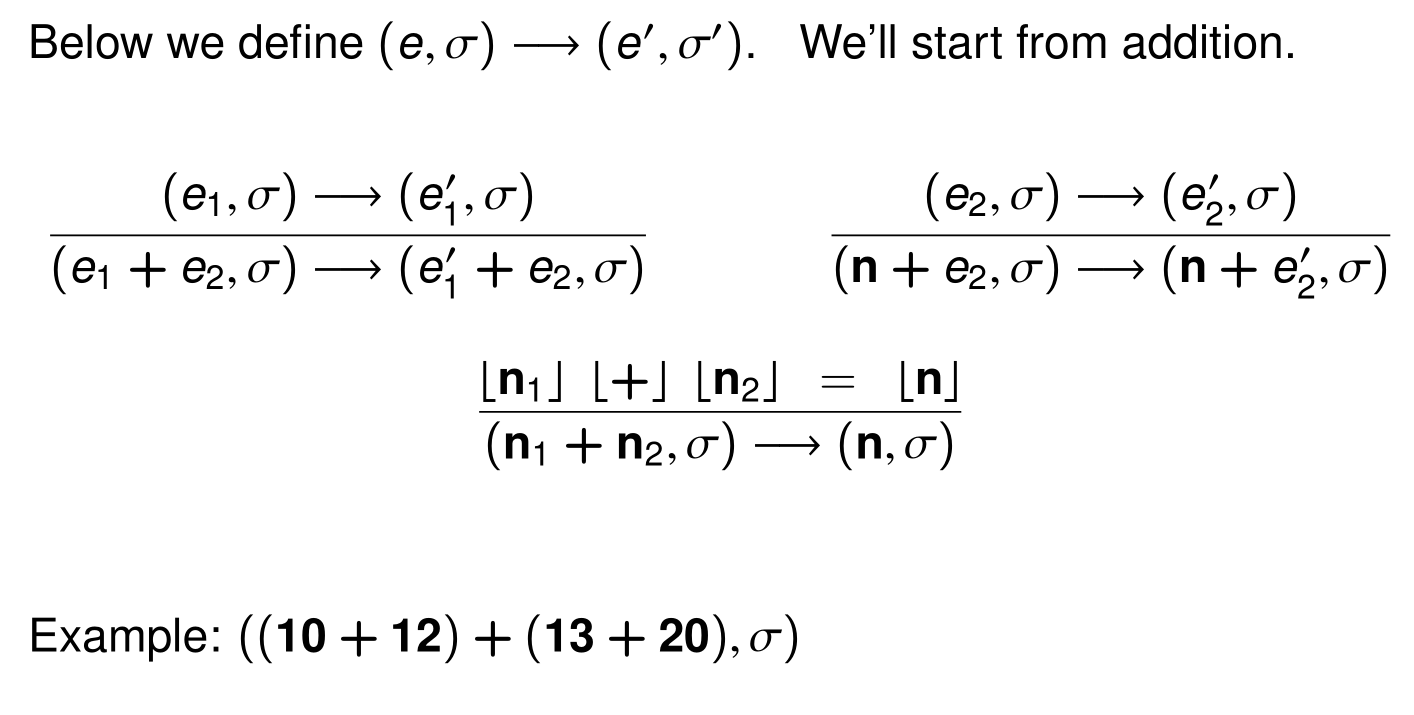
可以看到,这里的求值顺序是固定的,只能先计算左边项,再计算右边项。减法的定义同理,这里不再展开。
既然是命令式语言,那当然离不开State和对应的变量Var。对此,有以下转换规则:
(x,σ)→(n,σ)σ(x)=⌊n⌋
因此,我们现在有了加法、减法以及变量的规则。例子:
σ(x)=10,σ(y)=42(x+y,σ)→(10+y,σ)→(10+42,σ)→(52,σ)
对BoolExp,同样也有:

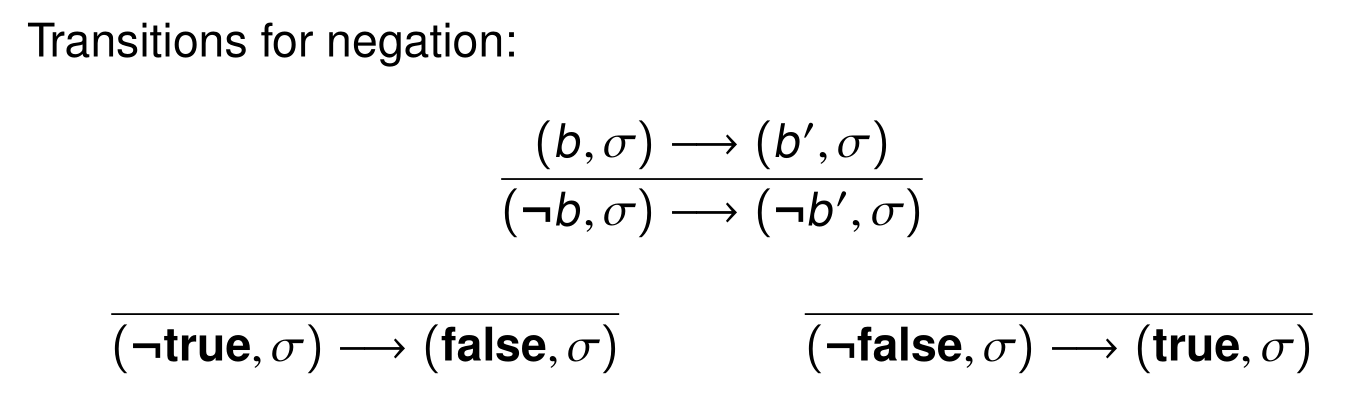

可以看到,这里的bool求值是没有短路求值的。若想要实现短路求值,需要将上面规则修改为:
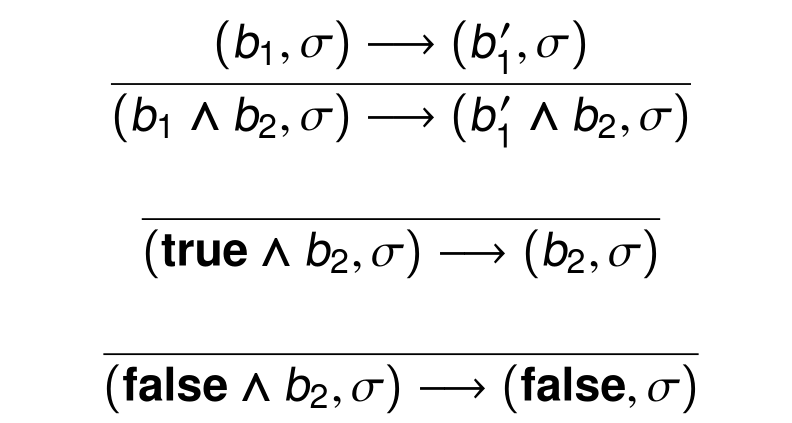
虽然我们在IntExp和BoolExp中都用→表示求值,但实际上这两种箭头分别代表着两种规则。但在本章范围内,将两者Overload写作相同的箭头是不会影响正常的Int with Int,Bool with Bool的求值过程的。
另外,接下来讨论的Statement中,箭头也不同于这两种箭头,不再赘述。
对Statement:
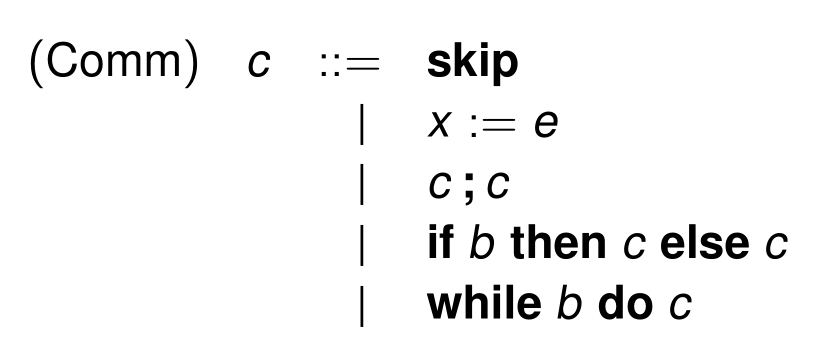
有以下规则
- Skip:
(skip,σ)→σ
- Assignment:
(x:=e,σ)→(x:=e′,σ)(e,σ)→(e′,σ)(x:=n,σ)→σ{x⇝⌊n⌋}
- sequential composition
(c0;c1,σ)→(c0′;c1,σ′)(c0,σ)→(c0′,σ′)(c0;c1,σ)→(c1,σ′)(c0,σ)→σ′
- if
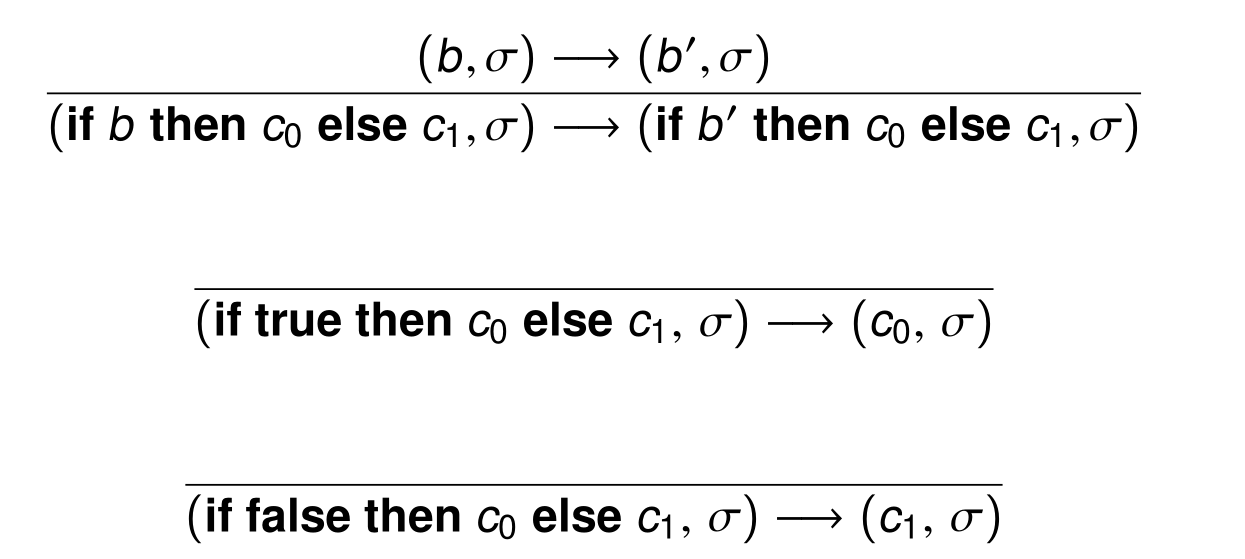
- while
(while b do c,σ)→(if b then (c;while b do c)else skip,σ)
这里while用if来构造,是因为若用while本体构造,那么while true的情况便陷入死循环。
Zero-Or-Multiple steps
类似之前对Lambda的定义,我们同样定义step的反射闭包→∗:
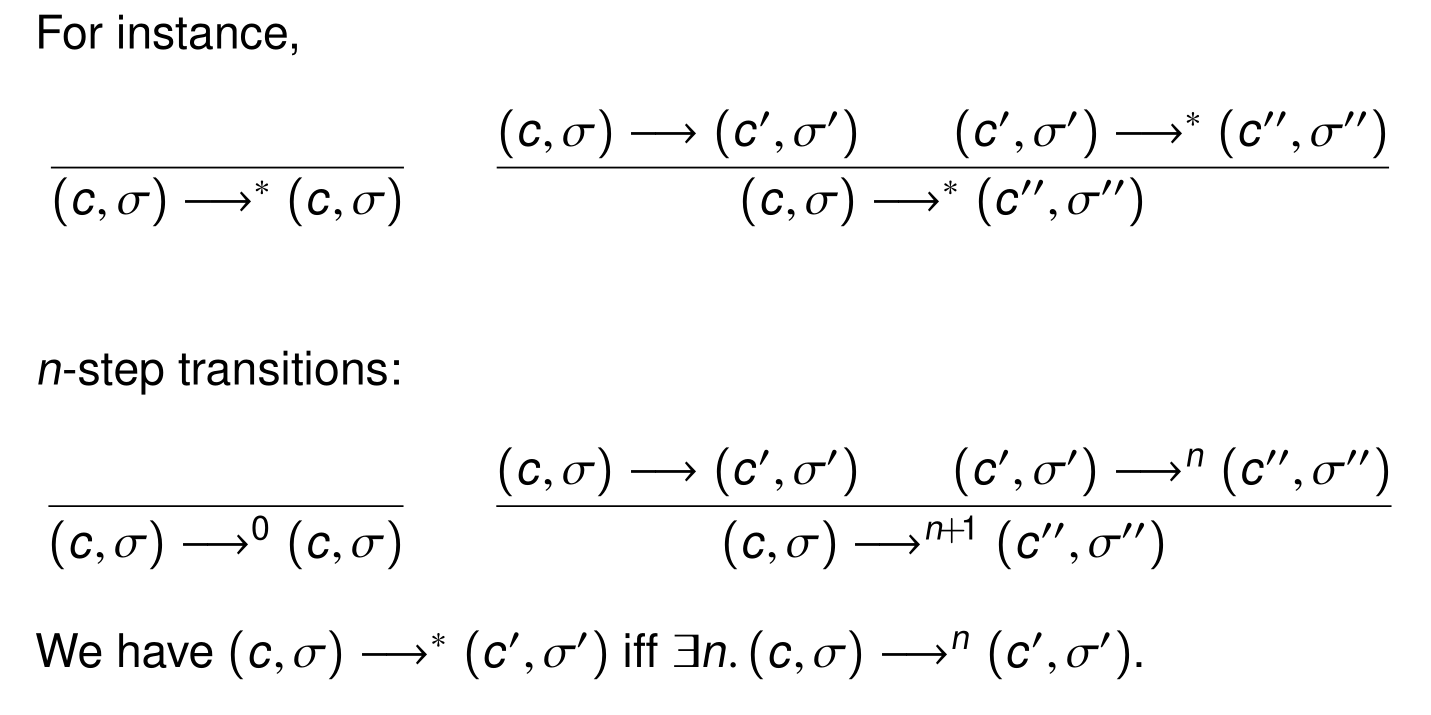
当然,对assignment引入的(c,σ)→∗σ′,同样也要定义类似以上的规则,这里略。
Some Fact
- Determinism,对所有c,σ,c′,σ′,c′′,σ′′,若(c,σ)→(c′,σ′)和(c,σ)→(c′′,σ′′),那么(c′,σ′)=(c′′,σ′′)。
- Corollary(Confluence):对所有c,σ,c′,σ′,c′′,σ′′,若(c,σ)→∗(c′,σ′)和(c,σ)→∗(c′′,σ′′),那么存在c′′′,σ′′′,使得(c′,σ′)→∗(c′′′,σ′′′)和(c′′,σ′′)→∗(c′′′,σ′′′)
- Normalization:任意的evaluation path最终都会evalueate一个normal form,即(n,σ)或(true,σ)(但Statement的transition是不能normalizing的,比如while true)
综上,Small-Step是很繁琐的,但很适合自动验证系统去机器式的求值/执行,或者说transition。
Variation
简化操作,直接定义求表达式的符号:

相当于跳过求值的Small step。
相对应的,也有Boolean的Variation:

while:

在之前的规则中,assignment会导致原本(e,σ)转换为单个σ,导致我们必须要为(e,σ)和σ都提供一套规则,现在我们设(skip,σ)为终止符号(即没有进一步的规则),其他规则求值的结果均为(skip,σ)形式。
(x:=e,σ)→(skipσ{x⇝n})[[e]]intexpσ=n
All Rules:
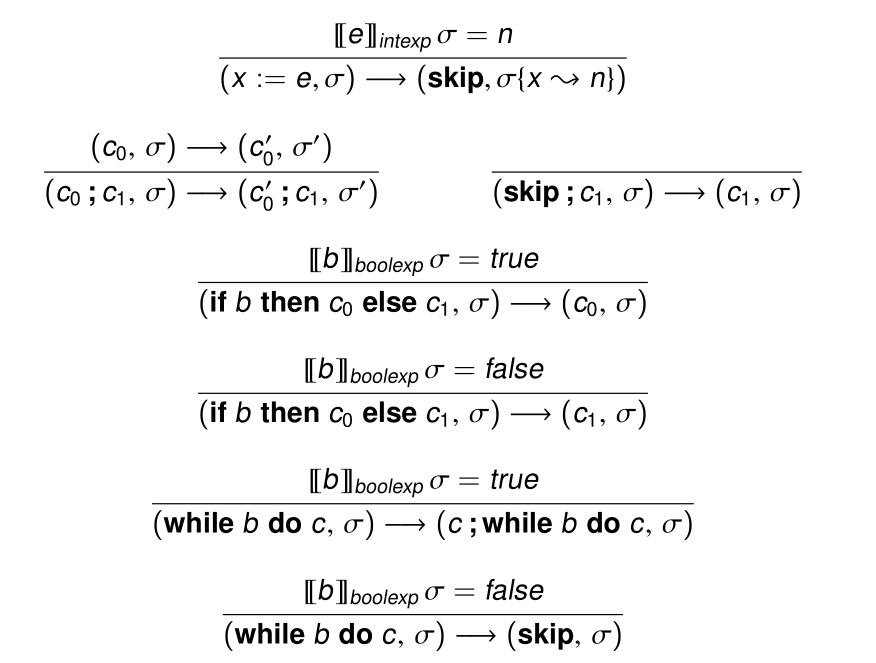
Go Wrong
引入新的configuration:abort,即标识非法操作,一旦触发abort程序便立刻终止,无法step。
比如,若给IntExp引入除法,当然要处理除以0的情况:
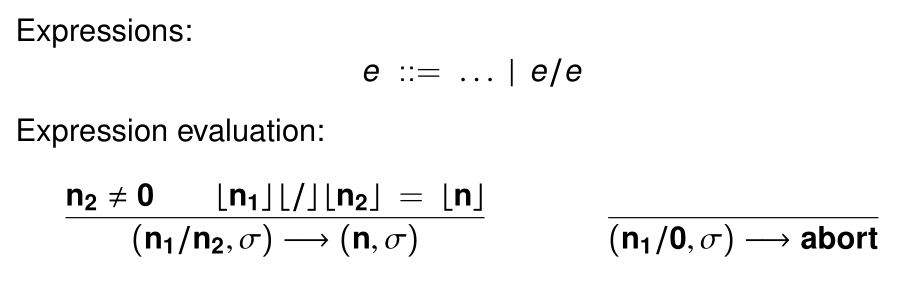
相对应的:
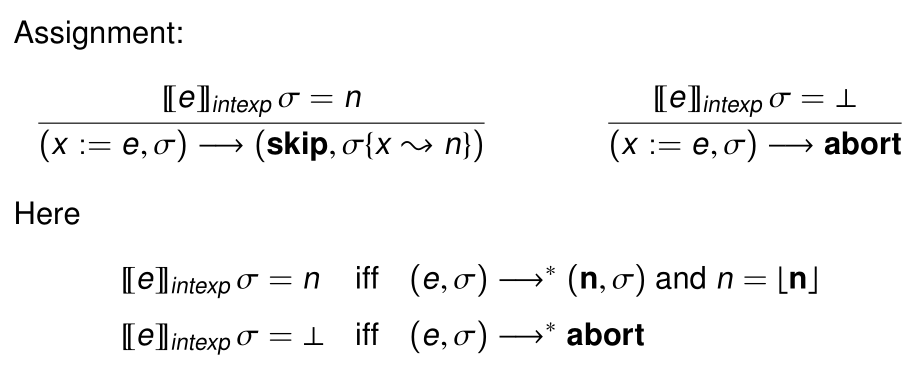

Local Variable declaration
Statement:
c::=...∣newvar x:=e in c
即:
(newvar x := e in c,σ)→(x:=e;c;x:=n,σ)σx=⌊n⌋
当然,这个定义在并行环境下是会被其他线程看见的,所以不那么准确。但本章没有并行,所以newvar的行为就类似于上面的规则。

Small-Step Contextual Semantics
即归约语义。
在SOS的讨论中,很多rule看上去都是类似的。现在我们将这些规则化为以下形式:

这种基于
(E[r],σ)→(E[e′],σ)(r,σ)→(e′,σ)
形式的式子中,r代表redex,即可以经一步reduction的expression/command:

而E代表evaluation context,即包含可以填一个sub-term的空洞的term。每个E都只有一个空洞,而空洞中填入的sub-term也是下一步要reduction的部分。因此,用evaluation context和redex的组合可以灵活的组合求值顺序,并精炼地表达求值规则。
因此,对contextual semantics,就是以下过程:
- 将当前term分为需要reduction的redex和evaluation context。
- 将redex r归约到t
- 放回原来的context,然后循环以上过程至终止。

对布尔值,也有类似的contextual semantics:

Big-Step Semantics
我们用⇓表示Big-Step语义。

Big-Step更像是一个递归解释器:

可以看到,Big-Step是不怎么管求值顺序的。
Some Fact about Big-Step
- Determinism:对所有e,σ,n,n′,若(e,σ)⇓n和(e,σ)⇓n′,那么n=n′
- Totality:对所有e,σ,存在n使得(e,σ)⇓n
- Equivalence to small-step semantics: (e,σ)⇓⌊n⌋iff(e,σ)→∗(n,σ)
Other Expression/Statement

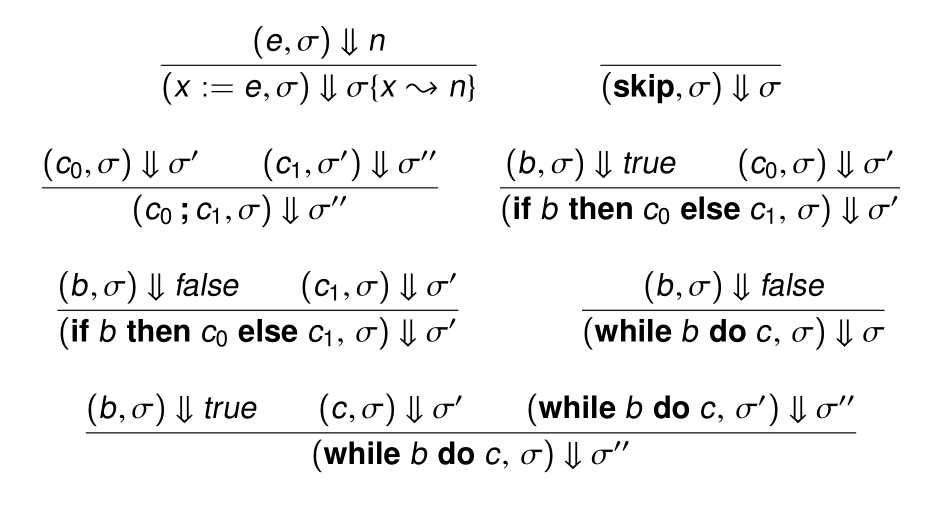
需要注意的是,Big-Step无法处理不终止的term,如无限循环。
Small-Step vs. Big-Step
- Small-Step可以更清晰的模拟复杂特性,如并发性、发散性(non-terminate)和runtime errors。但是,大部分情况下一步一步的讨论Small-step是没有必要的。
- Big-Step更接近于递归解释器,可以使证明更快,规则更少,所以没有final configuration(如get stuck(Skip)和无限循环)的程序看上去都一样,可能无法证明相关的问题。